While the "Law of the Minimum" makes a qualitative statement about the relationship
between a
growth factor and yield, the "Law of Diminishing Returns" (first formulated by Mitscherlich
in 1909)
describes this relationship quantitatively, i.e., mathematically.
Through pot experiments (using so-called Mitscherlich pots) with increasing doses
of a nutrient,
Mitscherlich found that yield did not increase linearly with nutrient supply, as would have been
expected according to the Law of the Minimum. Instead, a saturation curve emerged. He described
this curve using a differential equation, which states:
The increase in yield at any point on the curve is
proportional to the remaining gap to the
maximum yield – meaning the closer one gets to the maximum yield, the smaller the
additional yield becomes for the same further amount of nutrient added.
The observation that different nutrient elements, when applied in equal amounts, increase
yield to
different degrees led Mitscherlich to introduce an efficiency factor into the differential equation:
The efficiency factor is a measure of the yield effectiveness of the
nutrient. The higher it is, the
greater the yield effect of an additional unit of nutrient applied. It also depends on the plant species
and environmental conditions.
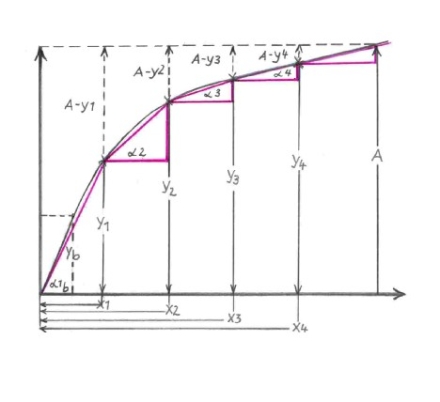
The curve below is a typical Mitscherlich curve with the formula:
dy/dx=c (A−y)
where
A = maximum yield,
y = current yield,
x = amount of nutrient applied,
c = efficiency factor
 Objections
to the law:
Objections
to the law:
- Time is not included as a variable
(over the course of the growth period, identical increases in a
factor can lead to different effects).
- The constancy of the efficiency factors
is not guaranteed (although they remain fairly constant
as long as all other factors are kept near optimal levels).
- The model primarily describes dry
matter yield (however, the maximum yield is not
automatically identical with the highest quality or the greatest environmental compatibility =>
this highlights the problem of differing production goals, both past and present).

